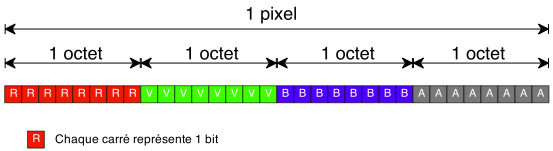
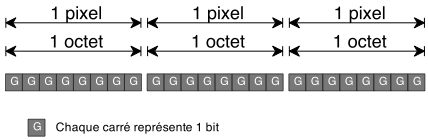
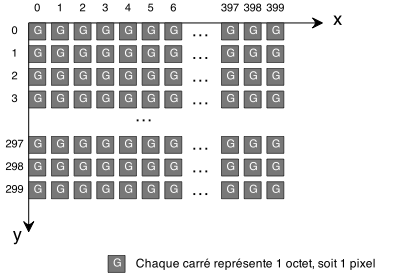
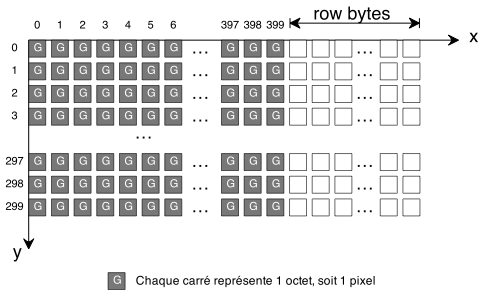
Quand on zoome on avant, notre ensemble fractal n'est plus très détaillé. Nous allons ajouter le réglage du nombre maximal d'itérations.
Modification de la couche Modèle
Jusqu'à présent, le nombre maximal d'itérations était codé en dur:
#define MAX_ITERATIONS 18
Nous remplaçons cette définition par la variable d'instance maxIterations
@interface CFRMandelbrotRender : NSObject {
…
unsigned char maxIterations;
}
Je l'ai typée en unsigned char, pour qu'elle soit comprise entre 0 et 255. En effet, notre bitmap en 256 niveaux de gris ne saurait de toute façon pas stocker l'image avec plus de précision. Inutile donc de calculer plus de 255 itérations.
Cependant, ce paramètre étant réglable par binding, il va être accédé par Key-Value Coding, qui ne gère que les entiers signés. J'ai donc rusé en utilisant des int pour les accesseurs:
- (void) setMaxIterations:(int)iterations
{
if(iterations > 255)
NSLog(@"-[CFRMandelbrotRender setMaxIterations:].
Le nombre d'itération doit être <= 255.");
maxIterations = iterations;
}
- (int) maxIterations
{
return maxIterations;
}
On n'oublie pas de l'initialiser dans la méthode -init:
maxIterations = 18;
J'ai conservé cette valeur de 18 par défaut.
Ajout des contrôles
Ouvrez MyDocument.nib. Ajoutez à la fenêtre un NSLabel, un NSSlider et un NSTextField.
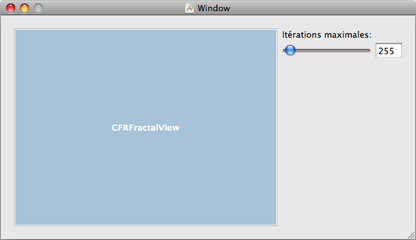
Réglez-les (avec le troisième onglet de l'Inspecteur) pour qu'ils restent scotchés au coin supérieur droit.
Configuration du NSSlider
- Réglez son minimum à 3
moins de trois itérations ne procure pas un résultat intéressant. - Réglez son maximum à 255
- J'ai réglé Current à 10
Peu importe, une fois bindé, il prendra la valeur par défaut du modèle, soit 18.
Configuration du NSTextField
- J'ai tapé la valeur 255 dedans… pour m'assurer qu'elle y rentre bien.
- Glissez un
NSNumberFormattersur le champ éditable.
Réglez ses contraintes: minimum à 3 et maximum à 255. Décochez Allows Float, nous ne voulons que des valeurs entières.
Binding
Contrôleur
Tout d'abord, pour binder, il nous faut un objet Contrôleur qui soit compatible avec les bindings. Comme nous gérons une seule instance du Modèle, nous utiliserons un NSObjectController:
- Glissez un NSObjectController dans MyDocument.nib
- Renommez-le en MandelbrotRenderController.
- Dans le premier onglet de l'inspecteur, réglez Class Name à CFRMandelbrotRender.
- En maintenant la touche Contrôle appuyée, tirez son l'outlet content vers l'instance de Mandelbrot Render (le cube bleu).
Binding du NSSlider
Sélectionnez le slider et passez sur le 4ème onglet de l'Inspecteur ("Bindings").
Pour binder la clé Value:
- Bind to: MandelbrotRenderController
- Controller Key = selection
- Model Key Path = maxIterations
Binding du NSTextField
Bindez le text field exactement de la même façon.
Résultat
Vous pouvez maintenant lancer le programme. Glissez le curseur Itérations maximales: l'ensemble reste le même. Allez sur la vue, et déplacez le repère ou zoomez: enfin, la nouvelle valeur est prise en compte.
Ce qui se passe est que le binding modifie effectivement maxIterations dans le CFRMandelbrotRender, mais cela ne provoque ni le recalcul de l'ensemble, ni l'affichage du nouvel ensemble.
Observation
Il faut un moyen pour que la vue sache que les paramètres ont été modifiés, que l'ensemble doit être recalculé, puis la vue rafraîchie. Une technique pourrait être de relier les actions du NSSlider et du NSTextField à la vue. Cependant, je pense ajouter par la suite des NSTextField pour permettre l'édition des autres paramètres, et cela va commencer à faire beaucoup d'actions. C'est pourquoi nous utiliserons ici la technique plus sophistiquée du Key-Value Observing.
Signaler le besoin d'une mise à jour
L'idée est que le CFMandelbrotRender sait quand il doit être recalculé: dès qu'un de ses paramètres de calcul est modifié. Nous allons lui ajouter une variable d'instance besoinMAJ, indiquant qu'une mise à jour est nécessaire:
@interface CFRMandelbrotRender : NSObject {
…
BOOL besoinMAJ; // Indique qu'une mise à jour est nécessaire
}
Ensuite, dès qu'un paramètre de calcul est modifié, nous mettrons besoinMAJ à YES:
- (void) setLargeurBitmap:(NSUInteger)largeurPixels
{
largeurBitmap = largeurPixels;
[self willChangeValueForKey:@"besoinMAJ"];
besoinMAJ = YES;
[self didChangeValueForKey:@"besoinMAJ"];
}
Notez l'encadrement par willChangeValueForKey: et didChangeValueForKey:. Ceux-ci sont indispensables au Key-Value Observing pour savoir que la variable besoinMAJ a changé.
Il faut faire de même dans les méthodes setHauteurBitmap:, zoomerDuFacteur:, decalerCentreX:y: puisqu'on y modifie les paramètres de calcul. Pour cette même raison, modifiez le setter de maxIterations:
- (void) setMaxIterations:(int)iterations
{
if(iterations > 255)
NSLog(@"-[CFRMandelbrotRender setMaxIterations:]. Le nombre d'itération doit être <= 255.");
maxIterations = iterations;
[self willChangeValueForKey:@"besoinMAJ"];
besoinMAJ = YES;
[self didChangeValueForKey:@"besoinMAJ"];
}
À la fin du rendu, repositionnez la variable:
- (NSBitmapImageRep*) bitmapImageRep
{
…
[self willChangeValueForKey:@"besoinMAJ"];
besoinMAJ = NO;
[self didChangeValueForKey:@"besoinMAJ"];
return bitmapRep;
}
Observer les besoins de mise à jour
Passons maintenant à la vue.
Contexte
Créons d'abord un contexte. De quoi s'agit-il ? D'objets uniques qui permettent d'identifier quel keypath a changé par une rapide comparaison de pointeurs, plutôt qu'une lente comparaison de chaînes de caractères:
static void* ContexteMAJRendu = (void*) @"ContexteMAJRendu";
Le contenu de la chaîne n'a aucune importance, puisque c'est le pointeur de l'objet que nous allons utiliser. On utilise habituellement une chaîne parce que c'est plus simple pour le débogage, mais n'importe quel autre objet peut faire l'affaire, pourvu que son pointeur soit unique.
Changements
Pour être tenu au courant des changements des clés observées, implémentons la méthode:
- (void)observeValueForKeyPath:(NSString *)keyPath
ofObject:(id)object
change:(NSDictionary *)change
context:(void *)context
{
if(context == ContexteMAJRendu)
{
[self setNeedsDisplay:YES];
}
}
Nous identifions le contexte et demandons l'affichage de la vue le cas échéant. Pour l'instant, il n'y a qu'une variable à observer, donc qu'un seul contexte, mais ça peut évoluer.
Nous n'avons plus besoin d'appeler setNeedsDisplay: ailleurs. Retirez-le des deux autres endroits.
Commencer l'observation
Ajoutez la méthode:
- (void) awakeFromNib
{
[render addObserver:self forKeyPath:@"besoinMAJ" options:0 context:ContexteMAJRendu];
}
Elle est appelée dès que tous les objets du NIB sont prêts. En particulier, ici, c'est l'objet render qui doit l'être. Nous ajoutons un observateur (=la vue), du keyPath besoinMAJ. Nous laissons les options par défaut, et fournissons le contexte à passer lors des changements.
Arrêter l'observation
Arrêter l'observation est toujours délicat, car il faut qu'elle ait cessé avant que l'objet observé reçoive un message -[dealloc]. Nous allons le faire quand la fenêtre se ferme.
- (void)viewWillMoveToWindow:(NSWindow *)newWindow
{
if(newWindow == nil)
[render removeObserver:self forKeyPath:@"besoinMAJ"];
}
Cette méthode est habituellement appelée lorsque la vue est insérée dans la fenêtre. Cependant, quand newWindow est nulle, cela signifie que la fenêtre va être close.
Et là ça marche ?
Vous pouvez essayer de lancer à nouveau l'appli. Cette fois-ci, ça fonctionne. À la prochaine !
Le projet Xcode complet à télécharger.
Renaud Pradenc
Céroce
 Quand on appuie sur la touche Contrôle, le curseur de la souris doit se transformer en flèches. Ceci, dès que le pointeur se trouve dans la vue.
Quand on appuie sur la touche Contrôle, le curseur de la souris doit se transformer en flèches. Ceci, dès que le pointeur se trouve dans la vue. Sinon, si le bouton n'est pas appuyé, le curseur est une main ouverte.
Sinon, si le bouton n'est pas appuyé, le curseur est une main ouverte.  S'il est appuyé, une main fermé.
S'il est appuyé, une main fermé.
 Cependant, les détails ne sont alors plus très présents. C'est parce que nous avons fixé le nombre d'itérations maximales trop bas. Heureusement, nous permettrons prochainement de modifier ce seuil.
Cependant, les détails ne sont alors plus très présents. C'est parce que nous avons fixé le nombre d'itérations maximales trop bas. Heureusement, nous permettrons prochainement de modifier ce seuil.